Gas transportation modeling at the cathode of a fuel cell with COMSOL Multiphysics®

Keywords

fuel cell, diffusion layer, serpentine, porous medium, cathode, pressure drop, oxygen, diffusion, current distribution
 

Context / Goal

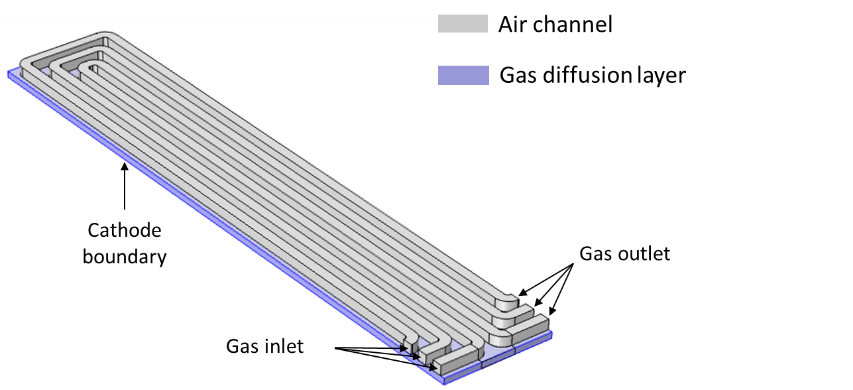
Oxygen is generally provided to the cathode of a fuel cell by means of serpentine-shaped channels. From this channel, the gas goes through a porous diffusion to finally get in contact with the cathode where it reacts to form water. The design of the serpentine pattern governs the fuel utilization, the current distribution and the pressure drop in the cell.

To ensure confidentiality, the present example is not a real client case. It is has been inspired from a Comsol tutorial. It describes the cathode air flow in a serpentine made of 3 channels and in the underlying diffusion layer. The objectives are as follows : 

  • determine the pressure drops in the serpentine,
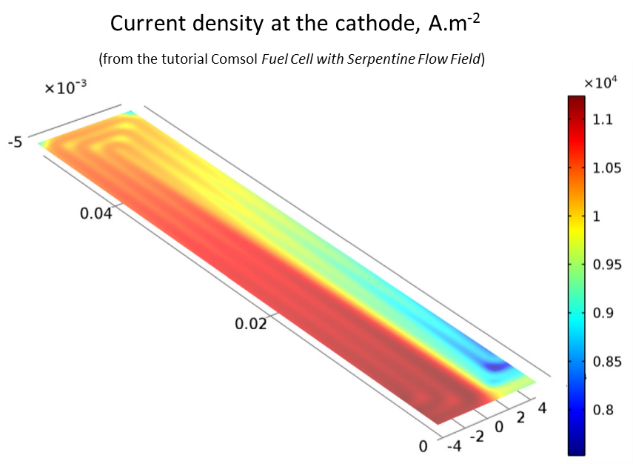
  • simulate the current distributions at the surface of the cathode, and
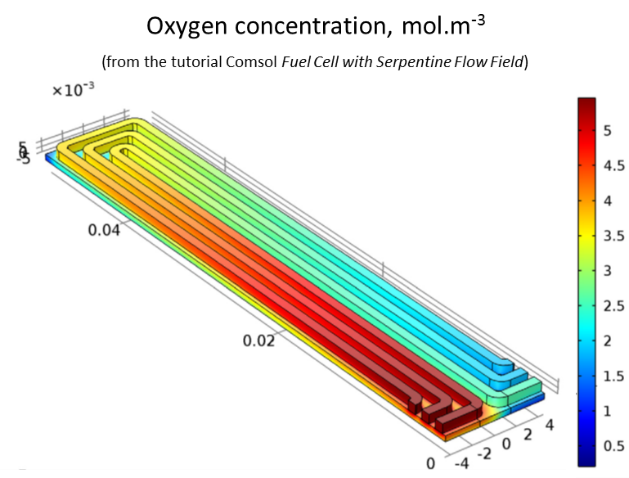
  • calculate the oxygen concentration in the system.
     

Geometry of the Serpentine Channel

The key points of this model are the following ones :

  • The air flow is calculated by the Darcy-Brinkman equations to describe porous media (diffusion layer).
  • The oxygen diffusion is understood through the Maxwell-Stefan equations, adapted to the description of motions in a gas mixture.
  • The currents at the surface of the cathode are described by an electrochemical kinetics law including the oxygen activity.

 

SIMTEC's Achievements / Results

Below are listed some results that are obtained with this model :

  • There is a significant pressure drop between the down-going and the up-going parts of the bottom channel.
  • As the gas circulates in the channels, the oxygen penetrates into the diffusion layer to react at the cathode; its concentration decreases progressively.
  • The current distribution at the surface of the cathode mirrors the concentration in oxygen; the reaction rate diminishes when the oxygen gets depleted.