Mots-clés

Matériaux composites, milieu équivalent, approche multi-échelles, homogénéisation, relocalisation, conduction thermique, milieu macroscopique-microscopique, alliages, milieux hétérogènes.

Contexte / Objectif

Des matériaux composites sont employés dans le but d’alléger un moteur à combustion interne d’une voiture de compétition. Certaines pièces, comme le collecteur d’admission d’air (Figure 1), sont fabriquées à base de textiles en fibres de carbone et d’une résine. Le collecteur d’admission est ainsi très léger et

résistant. Cependant, cette résistance dépend de la bonne liaison entre la fibre et la matrice en résine : lorsque le moteur est chaud mais que de l’air froid continue d’être a

dmis, des variations importantes de la température sont localement observées. Le but de cette étude est de déterminer l’ampleur de la dilatation thermique locale, qui pourrait se traduire par une désolidarisation de la fibre par rapport à la matrice.

Réalisations de SIMTEC / Résultats

Une modélisation numérique directe des échanges thermiques, considérant dans un unique modèle l’échelle microscopique des fibres et l’échelle macroscopique de la pièce entière, nécessiterait des moyens informatiques gigantesques et un temps de résolution très long En effet, la coexistence des deux échelles imposerait l’utilisation d’un maillage très raffiné.

Pour résoudre ce problème précisément et efficacement, SIMTEC a développé une méthode d’homogénéisation périodique, permettant de résoudre le problème macroscopique en tirant parti de la microstructure du matériau.

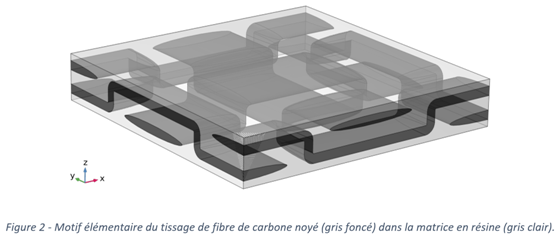
Cette méthode repose sur la définition d’un motif élémentaire du matériau composite (Figure 2). Des calculs spécifiques sur ce motif élémentaire permettent d’obtenir une conductivité K homogénéisée du matériau hétérogène.

Ici, cette conductivité dépend de la direction considérée :

La température dans l’ensemble du collecteur d’air peut être alors calculée précisément (Figure 3).

Ce calcul permet également de déterminer le gradient de température à l’échelle macroscopique dans tout le collecteur, Zm, et son maximum atteint à l’interface entre le collecteur et les cylindres du moteur.

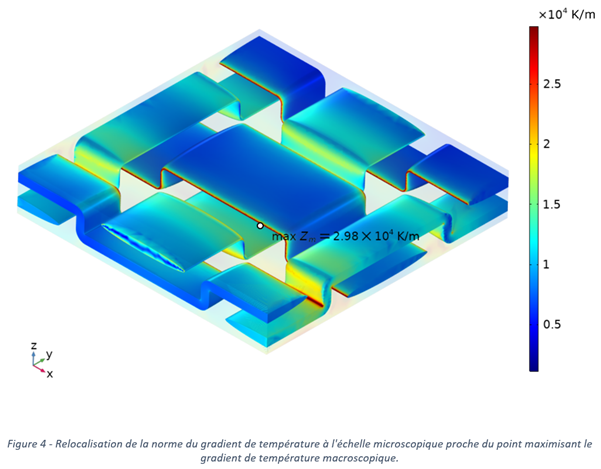
Cependant, cette valeur n’est pas représentative de l’amplitude du gradient à l’échelle de la microstructure (1.02e4 K/m vs 2.98 e4 K/m).

La méthode d’homogénéisation périodique permet de reconstruire précisément à l’échelle microscopique le champ de température et son gradient, permettant de déduire la dilatation des matériaux à l’interface fibre/matrice (Figure 4). A l’échelle microscopique, il existe ainsi des localisations à la frontière fibre/matrice dont la valeur extrême de gradient de température est trois fois supérieure au maximum du gradient apparent !

L’étude de SIMTEC permet donc de considérer le matériau à l’échelle macroscopique, tout en prenant en compte son échelle microscopique, pour quantifier les dilatations thermiques à l’interface fibre/matrice d’un matériau composite. Une telle approche permet, dans un second temps, d’optimiser les designs en minimisant le poids tout en assurant son intégrité dans le temps.

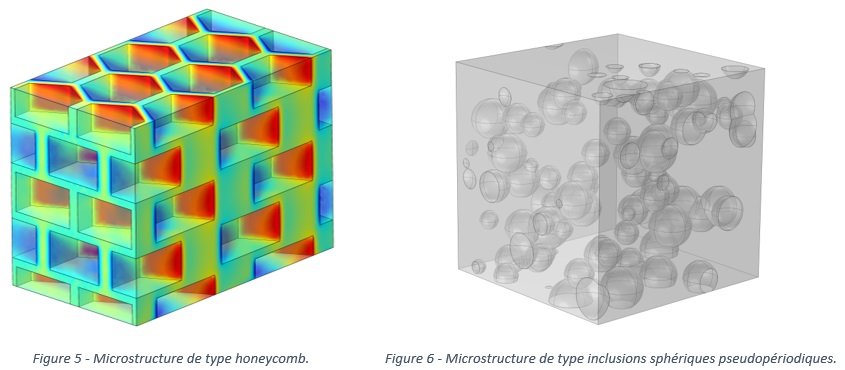
D’autres microstructures sont tout à fait envisageables, selon l’application considérée, comme les honeycomb (Figure 5) ou les structures pseudopériodiques (Figure 6).